Todavía
en la década de los 90´s del siglo anterior nos encargaban a los diseñadores
hacer este tipo de perspectiva para mostrar a inversionistas y/o prospectos de
clientes para la preventa de algún desarrollo arquitectónico. Casi siempre el
grupo objetivo para quien hacíamos esta comunicación eran personas que no
tenían una preparación técnica, pero que resultaba indispensable enamorarlos
del proyecto ya que sin ellos muchas veces era imposible llevarlo a cavo.
Objetivos de la unidad Al término de la unidad, el alumno:
Dibujará
perspectivas de formas básicas a un punto de fuga aplicando el método de la
geometría proyectiva, para calcular con exactitud la deformación de las
dimensiones a consecuencia de la variación de la distancia entre el observador
y el plano representado.
1. Concepto general de proyección central
Objetivos
específicos Al
término del tema, el alumno:
Proyección central
Existen
diferentes tipos de estímulos radiales como la gravedad y el calor, ya que
parten de un punto y se desplazan en todas direcciones, los estímulos luminosos
tienen también esta característica, la luz de una vela o el sol se desplaza en
todas direcciones y cuando dicha luz se refleja sobre cualquier punto de una
superficie nuevamente se desplaza en todas direcciones por eso se conocen como
estímulos radiales.
Este
fenómeno también es estudiado por la geometría, ya que es la manera natural
como vemos el mundo, en términos geométricos se dice; cuando el origen de los rayos proyectantes es un punto propio, da
origen a un tipo de proyección denominada central, aunque a nuestra
percepción los rayos del sol se desplazan paralelamente. Al ser reflejados por
un objeto ya se desplazan de manera radial haciendo nuestra percepción del
mundo cónica o central.
En
los tres esquemas que se te muestran a continuación; el tercero es el que corresponde
al concepto de proyección central ya que tiene un punto propio V, que es de
donde parten todos los rayos proyectantes.
Este tipo de proyección hace
que cuando vemos una calle desde el centro de esta las líneas paralelas de
banquetas, bardas, etc. Converjan en un punto que se encuentra en el horizonte
y que denominamos punto de fuga.
Como puedes ver en los
edificios, donde todas las líneas son verticales ascendentes el horizonte
parece estar en el cielo por lo tanto es mas un concepto de percepción que
geográfico.
No lo olvides el sentido de esta teoría es que seas
capas de engañar al ojo de tu receptor, en medios donde el soporte sea plano,
como casi todos; el monitor de la
TV o la computadora o impresos como revistas, libros y
carteles.
Actividades de
aprendizaje 1
Discute con tus compañeros lo siguiente:
1. ¿En
una misma imagen puede existir más de un sistema de proyecciones a un punto de
fuga?
2. En un
paisaje donde no hay líneas paralelas ¿Cómo funciona este tipo de proyecciones,
si es que existen?
3. ¿De un
mismo objeto se pueden obtener proyecciones a uno, dos o tres puntos de fuga
cambiando el punto de vista?
Para
que verifiques tu comprensión del tema califica las siguientes oraciones como
falsas o verdaderas:
1. Las
líneas paralelas de un sistema siempre tienen un mismo y único punto de fuga.
2. Las
proyecciones a un solo punto de fuga se ven cuando el observador se coloca
perpendicularmente a las líneas paralelas.
3. El
punto de fuga se encuentra en el horizonte.
4. Las
proyecciones centrales no tienen un punto propio.
5. Cuando la luz se refleja desde un punto de una
superficie lo hace de forma radial.
2. Conceptos básicos.
Objetivos
específicos Al
término del tema, el alumno:
Conceptos
básicos
La perspectiva a un punto de
fuga también es conocida como perspectiva
frontal debido a que el observador se coloca frente a la cara frontal del
objeto. Otra forma como se le conoce es perspectiva
paralela porque las aristas del objeto que se fugan son paralelas al eje de
visión del observador, auque se perciba en la perspectiva cono líneas
convergentes.
Punto
de fuga
El concepto más importante para la comprensión de
la perspectiva cónica es el de punto de fuga. Dicho punto es el lugar del
horizonte donde se juntan las líneas (paralelas) de fuga del objeto. Hay tantos
puntos de fuga como direcciones tengan las líneas (paralelas) en una representación, como en las fotografías que
se muestran a continuación:
Los
lados de los ángulos remarcan la dirección de las líneas paralelas que forman las
vides en el viñedo, se muestran en
diferentes colores para que notes como hay diferentes sistemas de líneas
paralelas en una imagen y fíjate como todos los vértices de los ángulos,
también llamados puntos de fuga siempre se encuentran en el horizonte.
Horizonte
La
línea de horizonte siempre coincidirá con el punto de vista del observador o
sea que si subes o bajas el horizonte también lo hará contigo, por tanto el
horizonte no siempre tiene que ser la superficie donde estas parado como a
simple vista parece ser.
En el
esquema se colocaron los ojos del observador a la altura del horizonte (la
imagen solo tiene fines ilustrativos ya que si dos personas de diferentes
estaturas están viendo el mar cada una vera el horizonte a su altura y su
acompañante puede ser solo un elemento más). Se ejemplifica el mar, ya que éste
es el horizonte real. Si a lo lejos ves arboledas o montañas estas no son el
horizonte, sino que son objetos que lo más probable es que estén por encima del
horizonte.
Entonces
si tu observas una caja y colocas tu vista exactamente al mismo nivel de la
tapa veras a está como si fuera una línea que se confunde con el horizonte, si
levantas un poco la caja y la ves desde la altura media de la misma, el
horizonte sigue estando a la altura de tus ojos por lo tanto no veras la tapa
ni la base solo la pared que esta frente a ti, esto es de particular
importancia cuando estas haciendo fotomontaje, debes de ser cuidadoso que al
tomar o seleccionar las imágenes la perspectiva de los objetos que piensas integrar
en la composición sea coincidente, dicho de otra manera piensa en la posición relativa de los objetos en cuanto
al observador y por tanto al horizonte.
Posición del observador
Siempre
que necesites hacer una perspectiva del tipo cónico tienes que considerar las
dimensiones del objeto y la distancia y altura a la que se encuentra el
observador, en la montea se dibuja respetando las escalas que intentas
representar en la realidad:
Ejemplo:
Siempre
que se aplique las dimensiones correctas de acuerdo a la realidad, la
perspectiva que obtengas será igual a lo que vez a simple vista.
Ocasionalmente
cuando se realizan perspectivas aplicando únicamente el método general pero sin
considerar las dimensiones se obtienen resultados extraños, ya que casi siempre
colocan al observador demasiado cerca y por lo tanto la vista se deforma
demasiado, como cuando tratas de ver un objeto que te lo acercas mucho a los
ojos no lo alcanzas a ver o a entender en plenitud.
No es lo mismo dibujar la montea que la perspectiva
ya que no cuentan con los mismos elementos ni tienen las mismas funciones y ni
siquiera están bajo la misma lógica de razonamiento.
Montea Se dibujara el mayor numero de medidas del objeto
en dimensión real, así como la distancia a la que se encuentra el observador y
altura ya que están en un sistema ortogonal, por lo tanto conceptos como punto
de fuga y horizonte aunque si se pueden dibujar no coinciden ni en
localización, el concepto ni la lógica del sistema.
Perspectiva Se dibujara la mayoría de las dimensiones en
escorzo o alteradas por la profundidad, la posición del punto de vista no se
encuentra, puedes encontrar el horizonte y punto de fuga si así lo requieres,
aunque con el sistema que te enseñaremos no es indispensable. Todo esto pasa
porque se trata de un sistema cónico de representación cuya finalidad es la de
engañar al ojo con la sensación de profundidad.
Como
puedes ver estamos haciendo uso de dos sistemas; el sistema de proyecciones
ortogonales que nos permite una razonada comprensión y un sistema cónico que
hace la percepción más realista.
Una
vez que comprendes los conceptos básicos, espero no se te dificulte
encontrarlos cuando los requieras en tu trabajo profesional, recuerda que estos
principios no solo se aplican cuando realizas soluciones con juego geométrico,
sino que en el uso de cualquier herramienta su conocimiento y manejo te permitirá
una mejor expresión.
Actividades de aprendizaje
Con el fin de que seas capas de
representar la realidad o una posible
realidad en la montea resuelve los siguientes problemas:
Problema
1.
Párate frente al salón fuera de
este a 2 m. ,
he imagina que no tiene la pared que se encuentra frente a ti, dibuja la planta
y el alzado en la montea a escala, todos los muebles y al observador. Acota las
dimensiones.
Forma de entregar:
·
Boceto de
las distancias con relación al observador y las dimensiones de los objetos.
·
Lámina en
limpio y a escala con instrumentos de la montea
Problema
2.
Tomando como base el problema 1.
Imagina que vas a modificar el orden de los muebles, dibuja en la montea como podrían
quedar, el punto de vista se mantiene como en el problema 1. Acota las dimensiones.
Forma de entrega:
·
Boceto de
las distancias con relación al observador y las dimensiones de los objetos.
·
Lámina en
limpio y a escala con instrumentos de la montea
Actividades de aprendizaje
Para que desarrolles tu
habilidad en la identificación de los conceptos básicos en una perspectiva a un
punto de fuga realiza la siguiente actividad:
1. Busca tres paisajes.
2.
Identifica los sistemas de perspectiva
a un punto de fuga
3.
Resalta con color las líneas paralelas
y los puntos de fuga
4.
Remarca el horizonte
3. Perspectiva del cuadrado.
Objetivos
específicos Al término del tema, el alumno:
Empleara el método geométrico de perspectiva a un
punto de fuga que le permite calcular todas las dimensiones que se encuentran
en escorzo con precisión para que sus ilustraciones sean más realistas.
Algunos artistas han
desarrollado métodos que son un tanto empíricos, posiblemente porque lo
delicioso del arte es su carácter lúdico, pero cuando se trata de competencia
empresarial en un mercado como el de hoy, difícilmente cabe esa posibilidad de
tanteo, es por eso que te mostraremos en
esta unidad un método muy rápido y en la
siguiente unidad otro que es poco mas laborioso.
Perspectiva
del cuadrado
Usaremos como lo hicimos en la
unidad anterior al cubo para ejemplificar los métodos, para este tema nos
resulta la proyección de varios cuadrados aunque solo nos ocuparemos de las
caras que vemos desde el punto donde se encuentra el observador.
A continuación un problema
ejemplo:
Como puedes ver el método es muy sencillo, lo único
que tienes que hacer es mantener un orden para que no te confundas. La
importancia de la proyección de este cuerpo es que puedes convertirlo en
prismas cuadrangulares y cuando las figuras no sean formadas por caras
cuadradas solo hazlas que sean contenidas en estos cuerpos que son fáciles de
hacer en perspectiva y dibuja los más complicados con relación a lo sencillo.
Actividades de aprendizaje
Como es indispensable que
conozcas y apliques el método para obtener la perspectiva del cuadrado te
pedimos que realices la siguiente actividad
Para que domines el método de
perspectiva cónica frontal: dibuja paso a paso desde la montea hasta obtener la
perspectiva del cubo a un punto de fuga como se te mostró anteriormente:
·
Dibuja y redacta cada uno de los pasos
en boceto.
·
Una vez que conozcas la solución y los
puntos significativos dibuja la lámina en limpio y ambienta.
4. Perspectiva del triángulo
Objetivos específicos Al término del tema, el alumno:
Perspectiva del triángulo
Posiblemente
por efectos de la estandarización industrial donde muchas de las materias
primas se adquieren en planos rectangulares, los espacios de nuestras casas,
escuelas y oficinas también suelen tener formas rectangulares parece ser que de
esa manera se optimiza el espacio disminuyendo el desperdicio, el caso es que
culturalmente estamos habituados a meter casi todo en formas cuadrangulares, ya
que siempre lo cuadrado nos es mas fácil de resolver. Lo veo con la mayoría de
los alumnos que siempre les gustan las cosas con formas caprichosas y
voluptuosas pero que al encontrar la dificultad de su representación y
producción deciden, según ellos, simplificarse las cosas haciendo todo cuadrado
aunque saben que funcionaría mejor con formas más dinámicas o estructuralmente
estables.
El
triangulo tiene esas características y si te es más fácil manipular el cuadro
toma en cuenta que a un cuadro lo puedes convertir en triángulos de manera
exacta o sea que el cuadro puede ser la matriz de muchos triángulos, de la
misma forma como el cubo puede ser matriz de pirámides.
A continuación tomaremos como inicio los cuatro
pasos que se siguieron para dibujar la
perspectiva del cubo, después se dibujaran dentro de este, formas triangulares
que consecuentemente estarán en perspectiva.
Problema
Dibuja la perspectiva frontal un prisma de base en forma de triangulo isósceles, la base triangular tiene en su base 1 m. y de apotema 1 m., recostado en el plano horizontal en su cara menor, siendo que el observador esta a 2 m. de distancia y dos metros de altura desde el plano horizontal.
Problema
Dibuja la perspectiva frontal un prisma de base en forma de triangulo isósceles, la base triangular tiene en su base 1 m. y de apotema 1 m., recostado en el plano horizontal en su cara menor, siendo que el observador esta a 2 m. de distancia y dos metros de altura desde el plano horizontal.
Solución
Se dibuja en la montea los datos.
Dibuja la perspectiva cónica frontal de un cubo que
tiene un metro por arista ubicado sobre el plano horizontal (cuando el punto de
vista esta a dos metros de distancia y de altura), una vez calculada la perspectiva del cubo, se resta el volumen que no corresponde al prismase remarcan los contornos del prisma y se ambienta.
·
Como puedes ver esta es la
forma más sencilla de representar el triángulo en perspectiva.
Creo que te resultara simple encontrar la
perspectiva del triángulo de esta manera, ya que lo único que tienes que hacer
es relacionarlo con formas que si tienen líneas paralelas, el
triángulo por si solo tiende confundir a las personas con poca experiencia.
Actividades de aprendizaje
El siguiente ejercicio tiene el
objetivo de que apliques el método para obtener la perspectiva del triangulo en
perspectiva cónica frontal.
Resuelve el siguiente problema:
Encuentra la perspectiva de un
prisma triangular, dispuesto de tal manera que ninguna de sus caras es paralela
a las líneas de fuga, el observador se encuentra parado a una distancia de 15 cm . Y lo mira a metro y
medio por encima del prisma.
·
Dibuja y redacta cada uno de los pasos
en boceto.
·
Una vez que conozcas la solución y los
puntos significativos dibuja la lámina en limpio y ambienta.
5. Perspectiva del círculo
Objetivos específicos Al término del tema, el alumno:
Empleara el método de perspectiva a un punto de
fuga visto en el tercer tema de está
unidad y lo hará extensivo en la perspectiva del circulo, usando al cuadro como
referencia.
5. Perspectiva del círculo
Objetivos específicos Al término del tema, el alumno:
Como con el triángulo
relacionaremos el círculo con formas cuadrangulares. El círculo es una
curva y por lo tanto lo que haremos es
encontrar su campo geométrico, que no es otra cosa que definir los puntos que
corresponden a dicha curva. Necesitamos los puntos que pertenecen al área del
cuadrado y a la circunferencia.
A continuación te presentare un
ejemplo claro de cómo son los pasos a seguir para emplear la perspectiva del
círculo:
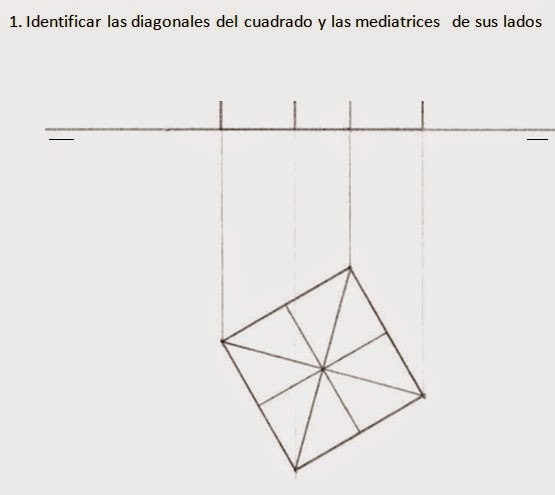
1 Dibuja el cuadrado que contendrá al círculo
en perspectiva, identifica las diagonales del cuadrado y las mediatrices de sus
lados.
2. Traza
un círculo tangente a los lados del
cuadro. Estos son los puntos que se
necesitan identificar para análogamente ubicarlos en la perspectiva de
cualquier cuadro. Los puntos de intersección de las mediatrices con los lados
del cuadro (puntos tangenciales entre los lados y la circunferencia) y la
intersección de la circunferencia con las diagonales.
3. Ahora se proyecta la
intersección de las diagonales y la circunferencia hacia los lados del cuadrado y se ubican las distancias Z que se
denominan con el mismo nombre porque por construcción siempre son iguales.
4. Después se dibuja este sistema en la
base de la proyección ya que esta no se encuentra en escorzo (en caso que lo estuviera
se dibuja a un lado adyacente). Si es necesario se puede realizar otro dibujo
donde solo se marque los trazos de la perspectiva que son necesarios, para evitar confusiones; lo
que se necesita es ubicar cuales son las distancias Z en las diagonales. Este sistema
se aplica para calcular la circunderencia o arco en cualquier tipo de
perspectiva.
Este sistema lo aplicaremos en el cubo para calcular 8 puntos de las circunferencias en escorzo.
Recapitulando, para representar circunferencias o
arcos de circunferencia tienes que determinar el campo geométrico que son los
puntos que pertenecen a la curva y a un plano cuadrangular que la contiene,
después encuentras la perspectiva del plano, ubicas la posición de los puntos
del campo geométrico y trazas las curvas sin olvidar que la curva es tangencial
a las aristas en los cuatro puntos tangencialmente y perpendicular a las
diagonales en los cuatro puntos. Con este método te será siempre práctico
encontrar la perspectiva de cualquier circunferencia o arco de esta.
Actividades de aprendizaje
Dicen que la practica hace al
maestro, por eso te pedimos que aplique el método para el trazo de la
circunferencia en perspectiva;
Proceso para la actividad:
1. Dibuja primero un cubo en
perspectiva y después los pasos
necesarios para la perspectiva del circulo (en los nueve que se mostraron los primeros
cuatro son para explicar el origen del razonamiento) en un boceto explicando el
por que de cada uno de los pasos.
2. Después pásalo en limpio en
albanene, cuidando la calidad y presentación sin errores y ambienta como si las puntas fueran redondeadas.
























No hay comentarios:
Publicar un comentario