Unidad 3 Perspectiva con dos puntos de fuga

Introducción

La importancia de la perspectiva con dos puntos de fuga es que es la otra forma natural de ver las cosas en nuestra ciudades tan llenas de formas rectangulares, al estar parado frente a la esquina de dos calles que se unen puedes notar como cada calle se fuga en diferente punto, una a la izquierda y la otra a la derecha de la esquina, y si hablamos de cuadriláteros como los mosaicos del piso de un cuarto también se fugan hacia dos puntos.

En esta unidad te mostraremos el método para determinar la deformación de los objetos por consecuencia de las proyecciones cónicas oblicuas también llamadas a dos puntos de fuga, este método es un poco mas laborioso que el que se te mostró en la unidad anterior, pero tiene la ventaja que te sirve para obtener cualquier perspectiva desde cualquier punto de vista esto se logra girando al objeto.

Con el fin de establecer conceptos que te deben ser comunes para la correcta interpretación del lenguaje empezaremos por explicar los conceptos de perspectiva oblicua y punto de vista para después continuar con la perspectiva del cuadrado como un polígono en donde se pueden contener y relacionar todas las demás formas; geométricas o biológicas, después mostraremos como este método aplicado al cuadro nos facilita la representación de triángulos y circunferencias.

Aunque ya existen programas para computadora como el 3D Studio que te permiten crear perspectivas cónicas a diferentes puntos de fuga, como profesional tienes la necesidad y obligación de tener conocimiento de causa para que puedas explicar a quien lo pregunte la razón y el fundamento de las cosas. Ya que entiendes la importancia de conocer la naturaleza de los principios iniciemos con entusiasmo el estudio de la perspectiva a dos puntos de fuga.

Objetivos de la unidad Al término de la unidad, el alumno: 
Dibujará perspectivas de formas básicas a dos puntos de fuga aplicando el método de la geometría con el uso de plano parámetral o de dibujo y plano auxiliar, lo cual le permitirá calcular con exactitud la deformación de las dimensiones a consecuencia de la variación de la distancia entre el observador y el plano representado y obtener la perspectiva desde cualquier punto de vista para que sean más realistas sus representaciones gráficas.

Tema 1. Perspectiva oblicua

Objetivos específicos Al término del tema, el alumno:

Reconocerá la perspectiva oblicua en un sistema de perspectiva cónica a dos puntos de fuga para que lo aplique en los siguientes temas de la unidad.

El Diccionario de Arquitectura y Construcción. “Sistema de proyección por el que un objeto tridimensional se representa mediante un dibujo en perspectiva en el que las caras paralelas al plano del cuadro están dibujadas a escala real y todas las líneas perpendiculares al plano del cuadro tienen una inclinación cualquiera distinta de 90°, a menudo inferior para compensar el aspecto distorsionado. También llamada oblicuo.” Como ya las vimos en la primera unidad al tratar la perspectiva caballera.

Perspectiva de dos puntos: “Perspectiva cónica de un cuerpo rectangular, de dos caras oblicuas con relación al plano del cuadro, por lo que las líneas verticales y paralelas al plano del cuadro permanecen verticales y las líneas oblicuas convergen hacia dos puntos de fuga, uno hacia la derecha y el otro hacia la izquierda. También llamada perspectiva angular”.

Esta es el tipo de perspectiva que nos ocupa por el momento y la razón de la denominación de oblicua esta dado por el hecho de que si metemos en un cuerpo rectangular los dos ejemplos que a continuación se muestran las caras de este están en posición oblicua con respecto al plano de dibujo, de tal manera que las líneas oblicuas que limitan estos planos convergen en dos puntos como se indica en la definición del diccionario. Como en este tipo de proyección lo que nos interesa es engañar al ojo con respecto al efecto de profundidad así las dimensiones se disminuyen al alejarse más del observador.

En la perspectiva Arts coche, las caras que se muestran se fugan en ambos sentidos como si se tratara de las caras externas del cuerpo rectangular.

En esta otra perspectiva denominada Arts casa 6, las líneas se fugan de forma cruzada, como si se tratara de las caras internas del cuerpo cuadrangular.

Un método rápido intuitivo pero no es exacto es el ejemplo problema que se te muestra a continuación.

Dibuja un cubo en perspectiva oblicua cónica.

1. Se comienza  por trazar la línea del horizonte y sobre ella señalar el Punto de Fuga 2 (PF2) y la vertical desde nuestro punto de vista. Desde el (PF2) se trazan dos líneas A y B, hasta los extremos de la vertical, sobre ellas se construyen una de las caras del cubo o hexaedro.

2. Desde el vértice superior izquierdo, se traza la línea C hasta que corte la línea del horizonte, donde se señala el Punto de Fuga 1 (PF1), tratando que, la línea C con la línea A formen un ángulo superior a 90º.

3. A continuación se traza, desde el punto PF1, la línea D hasta el vértice inferior izquierdo y que procede  a construir otra cara lateral.

4. Para construir la cara superior, se traza  desde los Puntos de Fuga (PF1) y (PF2) las líneas E y F, hasta los vértices superiores laterales.

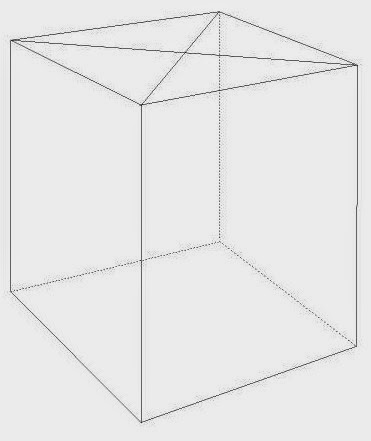
5. Una vez que ya se tiene formado visualmente el cubo, que sirve para comprobar que verdaderamente es un cubo hemos de dibujar las líneas y caras, opuestas que naturalmente no se ven, para ello trazaremos desde los puntos de Fuga 1 y 2, líneas hasta los vértices inferiores laterales (líneas azules H y G) para finalmente trazar la vertical J que une los vértices posteriores.

Aunque este método no permite calcular con precisión las deformaciones te lo muestro para cuando estés bocetando, y donde no requieras exactitud solamente aproximación y prontitud. Pero en el tema perspectiva del cuadrado te mostrare el método que te permite hacerlo con precisión matemática. Ten presente cada uno de los pasos que se te presento a lo lardo de la unidad y al finalizar te percataras cuando has aprendido.

Tema 2. Puntos de vista.

Objetivos específicos Al término del tema, el alumno:

Ubicará en la montea y en la perspectiva, el punto de vista con respecto al objeto, de acuerdo a los requerimientos de cada sistema, para que lo pueda relacionar directamente con la realidad que representa.

Tiene que ver con la posición del observador con respecto al objeto de representación, en la perspectiva cónica no se ve la posición del punto de vista, pero sabemos al menos la altura de este ya que es la misma que la línea de horizonte, aunque algunas vistas son mas naturales que otras, en ocasiones lo que se busca es dramatizar la imagen o sea que se busca mostrar las cosas como cotidianamente no las vemos. Dicho de otra forma mostrar lo que el ojo no ve.

En los siguientes dos ejemplos,  los puntos de vista adquieren su denominación por la posición que adquieren con respecto a la línea de horizonte, la tercera no tiene denominación especifica pero quise mostrar alguna otra alternativa que al momento de realizar composiciones,  y al tener diferentes posiciones con respecto al horizonte, es muy necesaria:

Vista a vuelo de pájaro

Es una forma retórica o artística de llamarla, en esta vista el observador se coloca desde arriba del objeto, que también podría ser un edificio de 40 pisos. Hablando de forma retórica puede crear diferentes interpretaciones como el de minimizar el objeto o personaje o el de engrandecer al observador, todo depende del espíritu de quien lo mira y el énfasis que se le de, a veces este se acentúa gracias al fondo que le puedas dar o del que lo puedas rodear.

Ojo de hormiga

En esta vista nos colocamos al ras del suelo o por debajo, al contrario del punto de vista a vuelo de pájaro, retóricamente este engrandece al objeto o minimiza al observador, también puede representar que se trata de un gran reto en nuestro futuro.

En la siguiente vista nos colocamos a la altura de la tapa del buró, para que el horizonte y la tapa quedaran en una misma línea:

Como podrás notar existen tantos puntos de vista como necesidades de mostrar algo tengas, por lo tanto antes de decidir el punto de vista de tu perspectiva piensa cual causará la mejor impresión a tu observador, es importante que consideres que como imagen forma parte de un texto visual que de pendiendo de su posición y espacio temporal de la lectura se tiene que dar diferente énfasis. A continuación te mostrare un ejemplo muy usado como recurso de representación, tanto así que cuenta con una denominación específica.

Vista traslúcida

Vista en la que una parte del dibujo se hace transparente y permite la representación de detalles que, de otra manera, quedarían ocultos.

El punto de vista lo puedes entender como el encuadre que haces con tu dibujo, recuerda que el objetivo es mostrar de manera más expresiva lo que la realidad no puede pero que sea comprensible y creíble para el receptor.

Actividades de aprendizaje

Discute con tus compañeros "Los Efecto emocional en la perspectiva del cine y los cómics”, aportando experiencias y observaciones de este tipo de perspectiva.

Contestando las siguientes preguntas he indicando el por que:

 ¿Cuáles son las imágenes o secuencias que más te han impactado?

¿Podrías indicar como lograr esa imagen o secuencia?

¿Por qué te es tan significativa?

Tema 3. Perspectiva del cuadrado

Objetivos específicos Al término del tema, el alumno:

Empleara el método geométrico de perspectiva a dos puntos de fuga que le permite calcular todas las dimensiones que se encuentran en escorzo con precisión para que sus ilustraciones sean más realistas.

La forma del plano que nos cuesta menos trabajo comprender su representación en perspectiva es el cuadro debido a que sus lados tienen dos direcciones, y por ser sus lados paralelos todos los puntos que los forman son análogos y las diagonales que unen sus vértices opuestos siempre forman ángulos rectos y la intersección de las diagonales coincide con la mediatriz de los lados, todas estas características hacen del cuadrado un plano geométrico que puede contener cualquier forma por caprichosa que esta sea y poderla manipular en perspectiva de forma más sencilla.

En el siguiente ejemplo se muestra la perspectiva exaedro (formado por 6 caras cuadradas) a dos puntos de fuga, en el sistema cónico, subsistema cuadro vertical con el método directo. Para el efecto te presento el siguiente problema como ejemplo:

 Dibuja la perspectiva cónica oblicua del cubo. (No olvides que el punto de vista tiene que estar frente a una esquina para que los lados le sean oblicuos, si lo colocas frente a uno de los lados la perspectiva se volverá frontal cónica.)

1. Dibujamos la montea, representando un cubo en planta y alzado y la ubicación del punto de vista. (Puedes dibujar todo a escala con la finalidad de que conozcas su relación con la realidad, para fines de enseñanza metodológica estos aspectos no se restringen y quedan como variables adaptables a cualquier caso.

2. Trazamos el plano del cuadro o del dibujo y el plano auxiliar. El plano auxiliar, paralelo al plano del cuadro, sirve para que no se encimen las proyecciones y la perspectiva.

3. Proyectamos desde la proyección del punto de vista en el plano del cuadro “v” a los puntos significativos de la planta.

4. En las intersecciones de los rayos proyectivos con el plano del cuadro trazamos horizontales al plano auxiliar.

5.       De las proyecciones al plano auxiliar, trazamos proyecciones a 45 grados a la línea de tierra, y en cada intersección con LT levantamos trazas verticales.

6. Trazamos rayos proyectivos del punto de vista “v´” a los puntos significativos del alzado del tetraedro.

7. De las intersecciones con el plano del cuadro, trazamos proyectantes en el alzado, paralelas a la LT, para encontrar las trazas de la perspectiva.

8. En las intersecciones horizontales y verticales de las proyectantes análogas, ubicamos los vértices y trazamos las aristas de la perspectiva.

En éste sistema la longitud de las alturas, anchos y profundidades se calculan en función de las vistas, donde aparecen en dimensión real. Si requieres ubicar los puntos de fuga prolonga las líneas de la tapa y la base y si unes esos puntos encontraras también el horizonte.

Recuerda que el método que acabas de ver te permite colocar al observador en puntos muy variados pero con cierto límite en ocasiones lo que más conviene es girar el objeto para no comprometer tanto al sistema.

Actividades de aprendizaje 

Como la práctica hace al maestro te pedimos que ejecutes cada uno de los pasos para obtener la perspectiva del cubo y de esa forma te quede bien entendido el método.

Para que domines el método de perspectiva cónica oblicua:

1. Dibuja y redacta cada uno de los pasos en boceto.
2. Una vez que conozcas la solución y los puntos significativos dibuja la lámina en limpio y ambienta.

Tema 4. Perspectiva del triángulo

Objetivos específicos Al término del tema, el alumno:

Empleará el método de perspectiva a dos puntos de fuga  visto en el tema anterior y lo hará extensivo en la perspectiva del triángulo usando al cubo como referencia.

Como recordaras un punto de fuga es hacia donde tienden las líneas paralelas de un determinado objeto en la proyección cónica, el caso del triángulo es especial porque no contiene líneas paralelas en sus lados por lo tanto lo relacionamos con una forma que si tenga líneas paralelas para facilitarnos el trabajo.

A continuación te indicaré la manera de construir una pirámide con base cuadrada, ya que cuatro de sus caras son triángulos en diferentes posiciones. Como mencionamos anteriormente existen tantos puntos de fuga como direcciones tengan las líneas que forman la perspectiva, para facilitar el trabajo calculamos la perspectiva de formas cuadrangulares a dos puntos de fuga y luego relacionamos los triángulos con el tetraedro.

1. Aprovechando el ejercicio del tema anterior, tomaremos la perspectiva del tetraedro que ya tenemos solucionado. Aplicando los ocho pasos de la perspectiva del cubo.

2. Localizamos el centro de la tapa del tetraedro, mediante diagonales.

3. A continuación se unen  los vértices de la base con el centro.

Como dijimos antes, la perspectiva sirve para engañar al ojo, y hacer creer que hay tres dimensiones cuando solo hay dos, por eso la perspectiva del triángulo tiene más sentido cuando se relaciona con otros elementos.

Como puedes notar cuando es un elemento tan sencillo como una pirámide podría resultar más rápido aplicar el método visto directamente sobre la pirámide, pero generalmente no te pedirán cosas tan sencillas y es entonces cuando se facilita realmente usar cuerpos cuadrangulares como referencia.

Actividades de aprendizaje

Es importante y  necesario que desarrolles tus capacidades psicomotrices te pido  que realices la siguiente actividad.

Para que domines el método de perspectiva cónica oblicua en el triángulo:

1.       Dibuja y redacta cada uno de los pasos en boceto (8+4).

2.       Una vez que conozcas la solución y los puntos significativos dibuja la lámina en limpio y ambienta la pirámide. 

Tema 5. Perspectiva del círculo

Objetivos específicos Al término del tema, el alumno:

Aplicará el método de perspectiva a dos puntos de fuga  visto en el tercer tema de está unidad y lo hará extensivo en la perspectiva del circulo, usando al cuadro como referencia.

Perspectiva del círculo

La perspectiva de curvas es indispensable para el estilo de diseño que actualmente es adquirido y considero que la tendencia se mantendrá mientras a la gente le guste sentirse cómoda con los objetos que usa cotidianamente, principalmente por causas ergonómicas. El circulo es la curva más significativa y gracias a conjugaciones entre arcos de circunferencia, puedes obtener prácticamente casi cualquier curva y que además conoces la esencia de cómo puede ser creada con perfección. No olvides que un espacio geométrico son todos los puntos que pertenecen a una curva y eso es precisamente lo que haremos, identificaremos los puntos que pertenecen al plano cuadrangular en perspectiva y simultáneamente a los curva vista en escorzo.

Como con el triángulo relacionaremos el círculo con formas cuadrangulares. Para ello primero las identificaremos.

1. Dibujar un cuadro perfecto, y en el tracemos diagonales y sus mediatrices.

2.  Tracemos un círculo tangente a los lados del cuadro. Estos son los puntos que necesitamos identificar para análogamente ubicar los en la perspectiva de cualquier cuadro. Los puntos de intersección de la mediatices con los lados del cuadro (puntos tangenciales entre los lados y la circunferencia) y las diagonales a partir de los vértices.

3. Ahora identifiquemos también la distancia z.

4. Estos conceptos los llevamos a la montea.

5. En los lados visibles de la perspectiva de hexaedro.

6 Con un curvigrafo o una pistola de curvas, tracemos las curvas que son tangentes a los lados en las intersecciones con la mediatriz y la tangente de la curva es perpendicular en la sexta parte de la diagonal.

Como pudiste ver a lo largo de estas tres unidades la forma más sencilla de de dibujar la circunferencia en escorzo es encontrando su relación con un cuadrado eso es lo único de lo que te tienes que cerciorarte que sin importar si parece un cuadro en perspectiva, en el espacio si tiene que serlo.

Actividades de aprendizaje

Como algo muy importante de esta materia es que sepas dibujar por eso te pedimos que practique haciendo todos los pasos que se te mostraron para la obtención de la perspectiva del circulo.

Para que incrementes tu habilidad en el trazo:

1. Dibuja los (8 + 5) pasos para la perspectiva de los tres círculos de las caras visibles del cubo, primero en boceto explicando el por que de cada uno de los pasos.

2. Después pásalo en limpio en albanene, cuidando la calidad y presentación sin errores.