En el
tema Clasificación y definición de perspectivas de la primera unidad, se
mencionaron y explicaron de manera general varios tipos de perspectiva entre
ellas la lineal y la de tono y matiz, esta última, se refiere específicamente a
las sombras y brillos que percibimos en el acto de ver y que hace más cercana
la experiencia a la realidad permitiendo así acercarse al objetivo de engañar
al ojo de que se trata de la percepción 3D en superficies planas como el
monitor de tu computadora, impresiones o fotografías.
El
desplazamiento de la luz por ser un fenómeno físico puede ser perfectamente
bien explicado por las matemáticas en su área geométrica y eso es lo que de
manera básica haremos en esta unidad, entender como incide y se refleja la luz
en los objetos, ya que es lo que vemos.
Empezaremos
por clasificar los tipos de luces de acuerdo a su incidencia, luego la cantidad
de luz que reflejan las superficies dependiendo del ángulo en el punto de
incidencia de la superficie que es lo que produce el efecto de tono y matiz y
en seguida estableceremos los métodos generales para dimensionar el alcance de
la proyección de las sombras, con el uso de las herramientas que nos
proporciona la geometría descriptiva y perspectiva.
Para veas la importancia revisa lo siguiente http://pijamasurf.com/2014/04/somos-otros-genial-video-muestra-como-tu-rostro-cambia-con-la-luz/
Objetivos de la unidad Al término de la unidad, el alumno:
Dibujara la sombra que proyectan objetos geométricos básicos aplicando el método de la geometría descriptiva y perspectiva, para dimensionarlas con precisión.
Tema 1. Método
Objetivos
específicos Al
término del tema, el alumno:
Reconocerá los principios geométricos aplicados en la
proyección de sombras de líneas verticales, con luz de sol o artificial y las tonalidades de la sombra de acuerdo al
ángulo de incidencia.
Tipos
de luz
Como
lo hemos dicho antes la luz es un fenómeno radial ya que desde su punto de
origen o el punto donde se refleja se desplaza en todas direcciones, esto es
fácil de apreciar en la luz artificial, como la que produce un foco o una vela,
pero cuando vemos la luz del sol la percibimos como si sus rayos viajaran de
forma paralela, estas son las razones que nos permiten afirmar, para nuestros
fines, que hay dos tipos de luces; las que se desplazan en todas direcciones de
manera cónica (luz artificial) y las
que se desplazan en una sola dirección de manera paralela (luz natural). En la montea estas luces la representaremos de la
siguiente manera:
La
luz artificial se representara por sus
proyecciones y su posición en el espacio y desde un punto propio. En el espacio
denominado “L” se proyectaran los haces de luz en todas direcciones, no así en
sus proyecciones horizontal y vertical (s y s´) donde dichos haces de luz solo
se desplazaran sus proyecciones sobre los planos horizontal y vertical
respectivamente.
La
luz natural o luz de sol que por la
distancia a la que esta de nosotros se le llama también punto en el infinito se representa por la inclinación de sus proyecciones (s´ y s)
con un ángulo cuyo vértice coincida con la línea de tierra aunque si el rayo es
paralelo al plano frontal no se forma dicho ángulo y para obtener la
inclinación de los rayos de luz en el espacio se lleva acabo su representación
al espacio S. Te recomiendo ver
primero cual es la dirección del rayo de luz en el espacio (S) con relación al
objeto del cual quieres dimensionar su sombra, para después encontrar sus
proyecciones cuando es necesario.
Para dibujar los haces de luz
en el caso de luz natural utilizaras las escuadras en primera posición ya que
dichos haces siempre serán paralelos a S, s.
Contrastes
de tono y matiz, intensidad de luz y sombra
Es
posible que conozcas una mesa de copia de imágenes con cámara fotográfica para
sacar ínternegativos, en ella, la cámara se coloca en posición perpendicular
central con respecto a la imagen a duplicar y las lámparas con un ángulo de 45º
con respecto a dicha imagen.
La
inclinación de las lámparas es para evitar reflejos (blancos) y áreas oscuras
en la copia, esto tiene su razón de ser. Cuando la luz incide sobre la
superficie de un cilindro o una esfera notaras que hay una zona donde se ve
blanco (tono) por el brillo que ocasiona la luz y a partir de donde la luz pasa
tangencialmente con respecto a la superficie toda esa zona ya no es iluminada y
por lo tanto no se ve porque es negra (matiz), los cambios de blanco a negro no
suceden de manera repentina, sino que lo hacen rítmicamente ya que el tono y el matiz de una superficie curva
obedece al ángulo en el punto de incidencia con respecto a la tangente o
sea que cuando la luz incide a 90º se produce brillo y a partir de donde el
ángulo es igual a 0º esta la oscuridad, donde el ángulo tiene una inclinación
de 45º se ve el color real del objeto y desde los 45º a los 90º se va aclarando
el color hasta llegar al blanco y a esto se le llama contraste de tono. De los
45º a los 0º el color se va oscureciendo hasta llegar al negro y a esto se le
llama contraste de matiz.
Para
lograr estos contrastes con pigmentos; el tono lo obtienes al agregar gris
claro o blanco al color puro (croma) y el matiz al agregar gris oscuro o negro
a dicho color. Para los tonos y matices intermedios los debes de hacer
proporcionalmente los porcentajes de cada pigmento en la mezcla proporcionalmente
a su variación de 45º a 0º
(color + negro o gris oscuro) o de 45º a 90º (color + blanco o gris claro).
Para
hacer más clara la aplicación de este concepto considera el siguiente ejemplo:
cuando vas a pintar un coche rojo compras un solo color de pintura y lo
esparces por toda la carrocería, sin embargo se ven en el coche brillos y
sombras, y si quieres hacer una ilustración del mismo, en tu paleta tendrás que
realizar las mezclas para que con sombras y brillos le des realismo y
profundidad al coche. Lo que pasa es que la luz incide sobre la superficie del
coche con diferentes inclinaciones y en la ilustración por ser un plano no
existen las inclinaciones, como en el prisma octagonal que se muestra a
continuación donde los rayos de luz inciden con diferentes inclinaciones con
respecto a cada cara.
Espero
que ya sepas como proporcionar la mezcla de los colores para lograr luces,
sombras y contrastes de tono y matiz que harán más realista tu trabajo ahora
solo lo tienes que poner a prueba hasta que domines la técnica.
Método
Como
se dijo anteriormente los contrastes de tono y matiz, son otro tipo de
perspectiva, que si los juntas con la perspectiva lineal cónica a uno o dos
puntos de fuga el realismo se incrementa y resulta más convincente para quien
lo mira. Por este motivo aplicaremos las sombras en objetos que ya dibujamos en
perspectiva cónica.
Empezare
por lo más sencillo que es la sombra que produce una línea vertical, determinada por un punto A en el espacio y su proyección horizontal a.
En el primer caso el segmento vertical esta a contraluz:
Este
método se aplica tanto con luz natural como artificial con la diferencia que en
el caso de la luz de sol todos los rayos en el espacio son paralelos a S y las proyecciones en el plano horizontal
de cada rayo paralelos a s en el
caso de la luz artificial todos los rayos parten de un punto propio F que también termina interceptándose
con su proyección casi siempre horizontal por ser la que coincide con el piso.
Como
puedes ver el principio es muy sencillo, porque solo se trata de un punto que
forma una línea vertical con su proyección, mas adelante te mostrare como todo
se va resolviendo aplicando siempre este método el numero de veces que sea
necesario dependiendo de la precisión que necesitemos para dimensionar las
sombras.
En los siguientes dos ejemplos te mostrare la
aplicación del principio anterior en un prisma con luz artificial y una
pirámide con luz natural.
Es
importante que aprendas a aplicar el principio básico y adaptarlo a las
necesidades de cada caso, empezamos con estos dos problemas censillos para que
te resulte obvia la aplicación.
Problema
1
Dibuja la sombra de un prisma
cuadrangular con luz artificial.
Como viste el principio siempre
se aplica con respecto a la vertical. Aunque en algunos casos una arista que coincida
con la vertical no existe, por eso es muy importante que visualices el carácter
abstracto del principio que siempre se aplica independientemente de los
elementos que se encuentren en el problema.
El siguiente problema es
ejemplo de cómo en ocasiones el vértice en el espacio no coincidirá con otro
vértice en la base.
Problema
2
Encuentra la sombra de una pirámide cuadrangular
con luz natural.
Otras
conceptos que debes considerar ya que en cualquier momento los puedes necesitar
para ubicar la posición de la sombra son que:
a)
Las dos proyectantes
forman un plano que corta a la imagen. O sea que se trata también de una
intersección y conocer esas líneas de intersección te permitirá determinar los
límites de las sombras.
b)
Aunque aquí
estamos obviando los pasos para obtener la perspectiva, recuerda que todo el
proceso es reversible y si algún límite de la sombra se te complica regresa a
la montea de proyecciones ortogonales y resulte en ella el problema.
Estos
dos puntos no los demostrare porque ya fueron tratados en su momento.
Si te
diste cuenta el principio siempre es el mismo. Encontrar la sombra de las
verticales y después unirlo de acuerdo a la lógica del objeto por lo tanto no
es difícil aunque si el proyecto es muy grande tendrá que ser laborioso y si no
organizas confuso, en los siguientes temas aplicaremos lo aquí expuesto.
Actividades de aprendizaje
experiencias y observaciones de
los conceptos mencionados. Toma como base las siguientes preguntas:
1. Coincidencias y diferencias
entre la luz natural y la luz artificial.
2. Aplicación de los contrastes
de tono y matiz en la comunicación visual.
3. Tu experiencia con pigmentos
en diferentes técnicas oscureciendo y aclarando colores.
4. Qué
pasa cuando hay muchas fuentes de luz.
Actividades de aprendizaje
- Dibuja y redacta cada uno de ejemplos en boceto; 1 de luz artificial, 1 de luz natural, 1 de tono y matiz, 1 de sombra de línea vertical a contra luz y 1 con luz detrás del observador, 1 para el prisma y 1 para la pirámide.
- Una vez que conozcas la solución y los puntos significativos dibuja la lámina en limpio.
Tema 2. Objeto compuesto
Objetivo específico Al
término del tema, el alumno:
El
cuerpo humano es una forma muy importante en perspectiva ya que permite
entender al observador la dimensión que puede tener un espacio (un cuarto o
sala) o un objeto (un meteorito o un celular), este no se incluye en el
programa de geometría porque lo ven en la materia de dibujo. Recuerda que cada
uno de los ejemplos que te presento, son para que los apliques en algún momento
y no se te dificulte en el momento de la actividad.
Pero
aquí lo tomaremos por la importancia que tiene que cuando integres figuras
humanas la sombra se genere bajo la misma lógica de todo el proyecto.
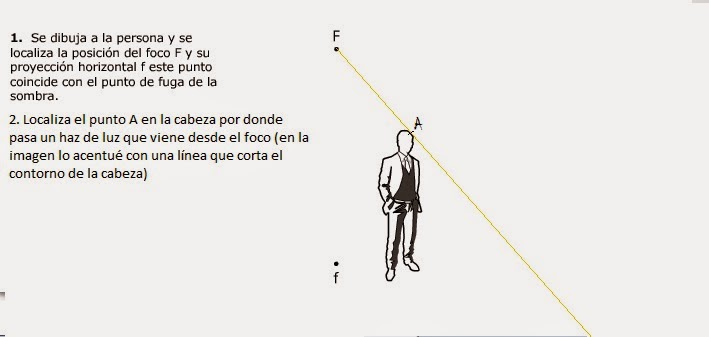
En el primer caso se determinara
la sombra de una persona a contra luz con luz artificial.
Actividades de aprendizaje
Dibuja y redacta cada uno de
los pasos en boceto 5 para la luz artificial
Temas 3. Plano en declive y 4. Planos escalonados
Objetivos
específicos Al
término del tema, el alumno:
Empleara el método geométrico para determinar la
sombra de un plano con declive y un escalonado y apreciar la deformación
originada por estos para hacer más realistas sus gráficos.
Plano
en declive
Esta
es otra forma que físicamente encontramos por todas partes, lo que le da su
relevancia, por eso también lo veremos como un caso específico, aunque para
fines didácticos lo trataremos separadamente.
En el
siguiente ejemplo te mostrare como determinar la sombra de un plano con declive
sobre el suelo y como se vería esta proyectarse sobre otro cuerpo.
Si en el que hiciste se te
complica recurre a la motea para que puedas ubicar la sombra en el plano
inclinado.
Planos
escalonados
Aunque
las escaleras difícilmente las encontraras de manera natural, en nuestras obras
arquitectónicas y civiles las vemos con profusión, aunque los profesionales del
diseño y la comunicación visual casi nunca diseñamos escaleras si las llegamos
a incluir en alguna estenografía o cuando hacemos una museografía o un ambiente
de marca y unas escaleras forman parte de la locación tenemos que considerarlas
como parte de nuestro proyecto de comunicación visual.
En el siguiente ejemplo te
mostrare como determinar la sombra de un plano escalonado sobe el suelo, a
contra luz con luz natural.
Actividades de aprendizaje
Dibuja
y redacta cada uno de los pasos en boceto;
8 de planos inclinados
6 de planos escalonados.
Una vez
que conozcas la solución y los puntos significativos
Temas 5. Planos sobre volumen, 6. Prisma sobre volumen, 7.Volumen con adición, 8. Giro
de volumen con adición y 9. Planos interiores.
Objetivo específico Aplicara el método geométrico para determinar las
sombras en plano sobre volumen, prisma sobre volumen, volumen con adición y giro y planos interiores para que encuentre
su relación en la realidad y calcule el alcance de estas.
Planos
sobre volumen
Aunque no hay muchos ejemplos de este concepto a
nuestra alrededor un objeto en forma de plano puede ser un espectacular, como
el que se muestra en la foto, que proyecta su sombra sobre una casa que es un
volumen.
También un papalote que
proyecta su sombra sobre cualquier cosa es otro ejemplo donde el plano es un
objeto. El plano no tiene tanta impotencia por los soportes que puedas
encontrar con tales característica, su importancia radica en que gran parte de
los cuerpos que encuentras en las cosas humanas se pueden descomponer en planos
como el techo y las paredes de un edificio, es por esto que se usa como caso
especial para ejemplificar la manera de calcular la sombra.
Ahora aplicaremos el método en
el primer ejemplo que tomamos en este tema aplicando luz natural.
Dibujaremos un plano en
posición vertical, como un espectacular, y un volumen cuadrangular.
6. Prisma sobre volumen
En el entorno urbano, hay muchos casos de formas prismáticas que reflejan su sombra sobre otros objetos, como las columnas que proyectan su sombra en la pared. Podemos dar muchos ejemplos, pero espero que con éste te des cuenta de la importancia de la aplicación del método en este caso específico.
A continuación te mostrare como se aplica el
método geométrico de las sombras en un prisma que proyecta su sombra sobre un
volumen.
No lo olvides, el secreto esta
en seguir la sombra de cada línea vertical por la superficie del volumen. Si
sigues con problemas para la determinación de los límites de la sombra piensa
que se forma un plano que corta al volumen como si fuera una barra de
mantequilla.
7.
Volumen con adición
Cualquier volumen al que se le
agrega otro elemento es un ejemplo de este caso especial de sombra, en la foto
que se muestra a continuación la casa es el volumen y el farol es la adición o
las rejas y marquesinas de las ventanas.
A continuación aplicaremos el método de sombras a
un prisma rectangular adicionado de oto prisma en su parte frontal, encuentra
la sombra que produce con luz de sol desde atrás del observador.
En este tipo de sombras no se
dibuja la parte debajo de la sombra sino la que esta por arriba todo es
siguiendo la lógica de construcción. Piensa que es como un techo o una
marquesina y creo que de esa forma te sera más cotidiano el concepto de este
caso específico de sombra.
Giro
de volumen con adición
El sol sigue su trayectoria
haciendo que las sombras se recorran, esto es lo que haremos, que el ángulo
formado entre la proyectante S y su
proyección s primero será recto y
luego mayor a 90º y veras como la sombra se recorre como pasa a lo largo del
día.
Para que no sigas copiando continua con los siguientes pasos aplicando el método como hasta ahora.
Como puedes ver puedes hacer
una animación de cómo la sombras van cambiando de posición conforme avanzan las
horas. Aunque es una figura retórica ya muy conocida, es una forma comprensible
para todos del paso del tiempo, tal ves con ello la gente no pueda calcular la
hora con exactitud pero se da una idea.
Planos
interiores
Cuantas veces no haz visto
entrar la luz por la ventana o puesta de tu casa, se percibe una sensación como
de esperanza o calidez, tal vez por eso se use tanto en las ilustraciones, en
eso consiste este tema, la manera de determinar hasta donde entra la luz y como
se ve en los planos que delimitan el interior.
En el siguiente ejemplo de
trazo se vera en un prisma hueco, hasta
donde entra la luz de una lámpara.
Cilindro
El
cilindro es otra forma muy utilizada como columnas,
las patas o la superficie de un mueble, es por eso que se hace relevante
ejercites la aplicación del método en cuerpos con estas características.
En el siguiente ejemplo determinaremos la sombra de
un cilindro a contra luz con sol.
De
cualquier superficie curva puedes proyectar su sombra solo tienes que descomponerla
en puntos y después convertirla en líneas verticales para encontrar la sombra
de cada una y después determinar por que puntos pasa el contorno de acuerdo a
la lógica de construcción.
Prisma sobre prisma triangular
Aunque
podría estar contenido en el concepto de planos con declive,
este es un caso que se presenta también con frecuencia en los techos de dos
aguas o en casas cuadradas que no están alineadas. En la foto se muestra como
la sombra se deforma sobre los planos inclinados con diferentes inclinaciones y
direcciones.
Para demostrar la aplicación del método usaremos un
prisma cuadrangular que proyecta su sombra en un prisma triangular acostado con
luz artificial.
Recuerda que en el prisma triangular
al igual que en la pirámide que se ejemplifico en los primeros temas, el punto
en el espacio tiene su proyección horizontal en la intersección del eje con la
base.
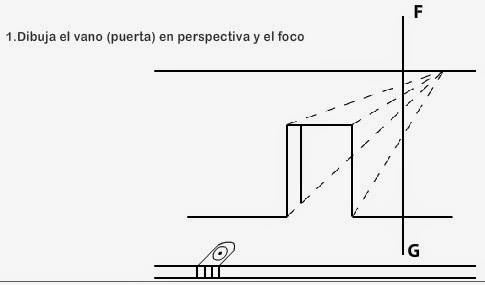
Muro
con vano
Aunque parece complicado solo
se trata de una pared con un orificio que puede ser para una ventana o una
puerta, que cuando se trata de construcciones con estilos clásico o rústico
suelen verse más interesantes.
En el siguiente ejercicio
encontraremos la sombra que proyecta el vano de un muro que se encuentra frente
a nosotros por un arbotante sobre la banqueta.
En este caso el secreto esta en localizar puntos
intermedios como en D que se encuentra en la fachada que produce la sombra en
el plano interior del vano, fíjate como encontramos una proyectante que
coincidiera con la línea Cc y en la intersección de dicha proyectante con la
proyección de la línea ab, localizamos la proyección d para luego ubicar en el
espacio D, en este caso el método se aplicó de manera reversible, que es la
principal característica de todos los métodos matemáticos.
Prisma
sobre terreno hundido
En colonias ubicadas entre colinas este caso
también es común, aunque nada recomendable ya que la construcción queda a dos
aguas o sobre un arrollo y es seguro que algún día se inundara, pero existen
casos como las columnas de un puente que resultan indispensables
estructuralmente, como las del ejemplo donde las columnas tienen forma de
prismas y su base esta en lo mas profundo del terreno hundido.
Para terminar los casos significativos parta la
aplicación del método de sombras tenemos este donde el prisma esta en el fondo
de un campo hundido.
El secreto esta en mantener
bien claro donde se encuentra el piso (parte más baja) y desde ese nivel hacer
todos los cálculos.